| Wenn Ihr Euch diese Anleitung ausdrucken wollt, dann HIER Klicken. Hinweis: Am besten immer nur im "Draufsicht-fenster" benden. (also da wo die xz-Achsen zu sehen sind)! In den anderen Fenstern gibt es immer Probleme. Immer nach links oder rechts biegen - nicht nach oben oder unten! Zuerst mal das Bild: (klicke auf das Bild!) 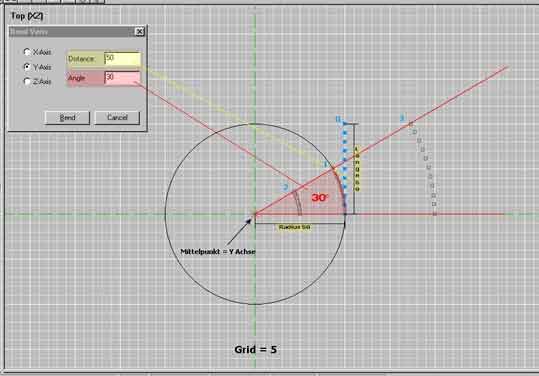 Statt eines Raumes habe ich hier der Einfachheit halber nur eine Linie aus Verts benutzt. (die kleinen blauen Quadrate) Um ein akzeptables und halbwegs voraussagbares Ergebnis zu erzielen, ist es wichtig die Werte für >Distance< und >Angle< richtig anzugeben. Die >Distance< ist der >Radius< eines gedachten Kreises um die Bendachse (hier Y). Sie sollte identisch sein mit der >Länge< des zu bendenden Raumes. Im Bild sind die zueinander gehörenden Werte gelb unterlegt. >Angle< entspricht dem Kreiswinkel in Grad um den der zu bendende Raum um den >Mittelpunkt< gebogen werden soll. Im Bild sind die zueinander gehörenden Werte rot unterlegt. Das Problem das die meisten Leute haben ist, das nach dem benden die Länge des gebendeten Raumes nicht mit den vorher angenommenen Maßen übereinstimmt. Die Endlänge hängt nämlich von der Entfernung (>Radius<) der Verts zum >Mittelpunkt< ab. Dies kann man im Bild deutlich erkennen. 0 entspricht den ungebendeten Verts. Alle Verts (>1< , >2< und >3<) wurden mit identischen Werten gebendet (50/30). Allerdings jeweils mit unterschiedlichem >Radius< vom >Mittelpunkt< (die Verts von >0< wurden dazu jeweils an die entsprechenden Positionen verschoben). Demzufolge wird die >Länge< mit zunehmender Entfernung auch immer größer obwohl der Winkel (>Angle<) immer 30° bleibt. Rückt man näher an den >Mittelpunkt< heran, werden die Verts entsprechend gestaucht. Die Krümmung des gebendeten Raumes bleibt jedoch in allen Fällen gleich.(30°) Problematisch ist allerdings die Vorhersage der Endlänge. Gemeint ist damit die Strecke die im Bild mit >Länge< bezeichnet ist. (im Grunde genommen also die Höhe des Raum-Endes über der z-Achse - im Bild mit "Länge" bezeichnet) Gibt man bei >Angle< 90° ein so ist diese Endlänge = der Entfernung zum >Mittelpunkt< Bei anderen Winkeln klappt das aber nicht !!! Noch problematischer wird es wenn man bei >Distance< einen Wert angibt der kleiner oder größer als die >Länge< des zu bendenden Raumes ist. In dem Fall wird das Ergebnis NICHT!!! dem erwarteten und eingestellten Winkel (>Angle<) entsprechen. Könnt es gerne probieren. Um also vernünftige Ergebnisse zu bekommen, muss man vorher wissen wie groß die endgültige Krümmung des Endraumes sein soll (= >Angle<) und man muss wissen wie lang der (ungebogene) Ausgangsraum ist (= >Distance<). |
| Um dem Endraum nun die gewünschte >Länge< zu geben, (weil man z.B. den Anschluß an einen bereits vorhandenen Nachbarraum herstellen will) muss man den Ausgangsraum "lediglich" in die richtige Entfernung zur Bendachse (>Mittelpunkt<) bringen. Diese Entfernung kann man nach folgender Formel berechnen c=a/sin(alpha) ... weil Entfernung zum Mittelpunkt = c = Hypotenuse des rechtwinkligen Dreiecks, welche gleichzeitig den Radius um Punkt A (hier der Ursprung der Drehung) durch Punkt B darstellt. (die kürzere Kathete ist immer a, Punkt A und Winkel Alpha liegen immer der jeweiligen Seite a gegenüber)
Entfernung zum Mittelpunkt = 50 Die gewünschte Endlänge war 25. Die Entfernung zum >Mittelpunkt< muss also 50 betragen. Schaut euch das Bild an - die Werte stimmen. Vielen Dank an Floyd der diese Formel für mich herausgesucht hat. Um für eine bestimmte Entfernung vom >Mittelpunkt< die Endlänge des Raumes zu berechnen, braucht man die Formel nur ein wenig umzustellen. In diesem Fall würde sie lauten: c x sin(alpha) = a Wem das alles zu viel Rechnerei und Formelei war, der achte eben halt wenigstens darauf, bei Angle und Distance die RICHTIGEN Werte einzugeben. Dann klappt's auch mit dem biegen ... ;) Viel Spaß beim Benden wünscht euch (LL)Dark |